散布図を描くときのコツ!
卒業論文や修士論文などで2つのデータ間の関係を検討したいときには、散布図を描いてみることをお勧めします。

2つのデータの関係とか難しそうで、散布図ってなんか苦手!
たしかに、散布図は、円グラフや棒グラフ、折れ線グラフよりも親しみにくいかもしれません。
総務省統計局の「なるほど統計学園」でも、散布図は上級編で紹介されています。
なるほど統計学園 グラフの作り方(上級編) グラフの種類 散布図

とはいえ、上のリンク先、児童・生徒向けの学習サイトです!
ということで、以下、「なるほど統計学園」より、もう少し大学生っぽい散布図を描画してみます。
新しい学習方法を検討するために散布図を描く
散布図は、2つのデータの関係を検討したいときに役立ちます。

「最高気温が上がるとエアコンの販売台数が増える」みたいなときだ!

たしかに、最高気温が上がるとエアコンの販売台数は増えそうですね!
ただし、研究の場では、明らかに関係がありそうなデータを描画するのではなく、何かしら関係がありそうなデータを描画するケースで使う場合が多いです。

「関係があるかどうかよくわからないものの散布図を描く」ってこと? 難しそうだね!
散布図を描画するときは「どのような関係を検討したいのか」という目的を明確にすることが大切です。
その目的のために、何と何の関係を描画するか工夫します。
うまく工夫できると、隠れていた関係が見えてくることがあります。
ここでは、仮のデータを使って
1. 新しい学習方法を実施する前の事前テストの点数と、実施した後の事後テストの点数
2. 新しい学習方法を実施する前の事前テストの点数と、新しい学習方法を実施したあとの事後テストとの得点差
の散布図を描いてみましょう。
散布図を描く目的は「新しい学習方法は、テストの得点に関係するかどうか検討すること」です。
使用したデータ(仮のデータ)
40人の学生に新しい学習法を試みました。
下記の表は、新しい学習法を試みる前と試みた後のテストの点数の一覧です。

事前と事後のテストの点数を使った散布図
まず
1. 新しい学習方法を実施する前の事前テストの点数と、実施した後の事後テストの点数
の関係をみてみましょう。
散布図自体は、Excelのグラフ描画機能を使って簡単に描くことができます。
(横軸が事前テストの得点、縦軸が事後テストの得点)
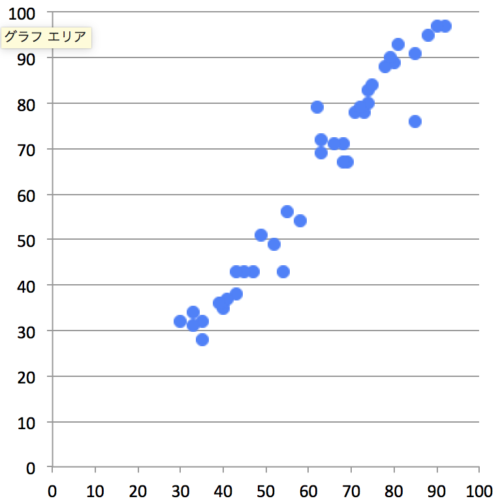
Excel(Microsoft Office for Mac 2011)を使用

なんか、いい感じの散布図が描けてる!

確かに、正の相関関係!っぽい、いい感じのグラフが描けていますね
でも、この散布図で表していることは「事前テストで点の低い学生は、事後テストでも点が低い」「事前テストで点の高い学生は、事後テストでも点が高い」という関係だけです。
これでは、新しい学習方法とテストの点数に何かしら関係があるかの検討はできません。
得点差を使った散布図
次に
2. 新しい学習方法を実施する前の事前テストの点数と、新しい学習方法を実施したあとの事後テストとの得点差
の関係をみてみます。
まず、仮のデータの事前テストと事後テストの得点差を求めてみます。
それから、事前テストの得点と新しい学習方法を試みた後の事後テストとの得点差の関係を散布図で描画します。
また、散布図が見やすくなるよう、得点がマイナスの場合と得点がプラスの場合に分けて描画しています。
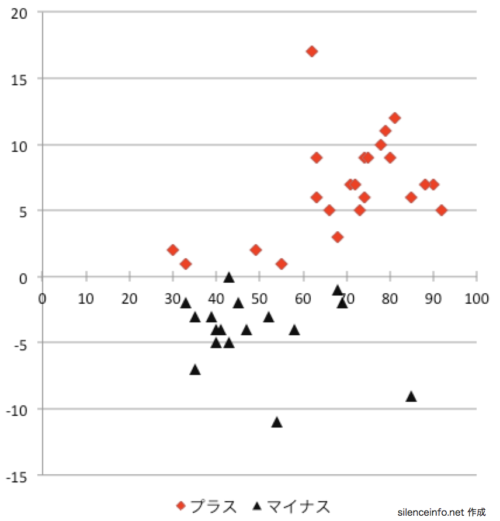
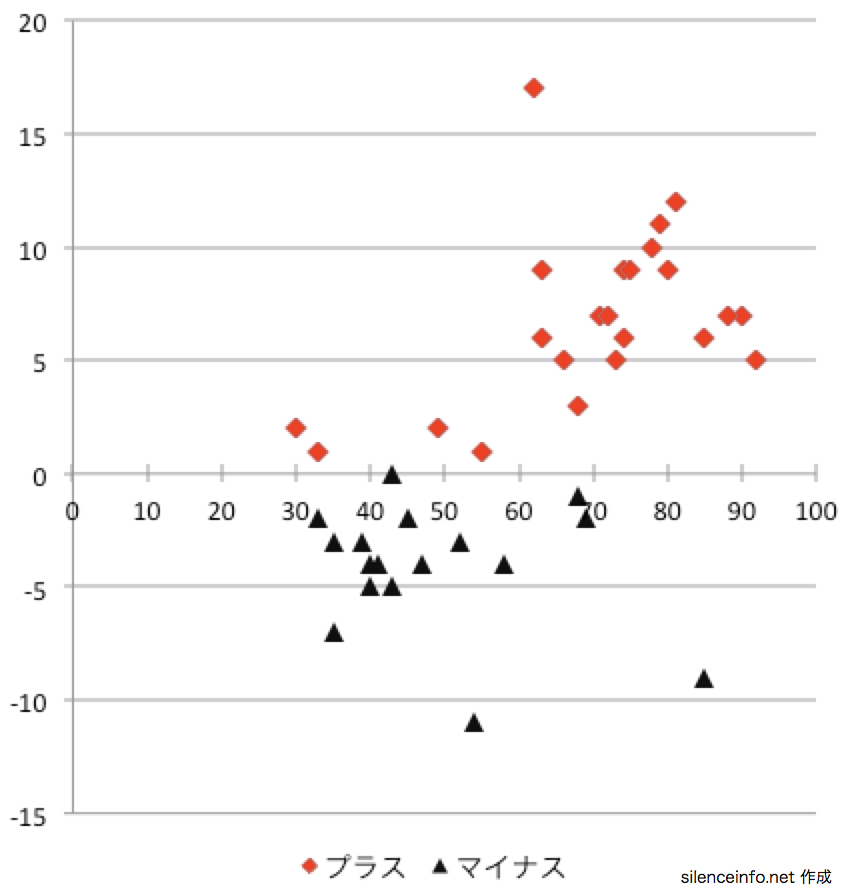
・得点がマイナスとは、事後テストで得点が下がったケース
・得点がプラスとは、事後テストで得点が上がったケース

赤のマイナスと黒のプラスがすごく偏ってプロットされてる!
上のグラフからは「もともと高得点を取ることができる学生に新しい学習方法を試みると、得点が上がる傾向」「もともと低得点しか取れない学生に新しい学習方法を試みると、得点が下がる傾向」があるといえそうです。
散布図を描く目的は「新しい学習方法は、テストの得点に関係するかどうか検討すること」でしたから、この散布図を使うと何かしら関係があるといえそうです。
このように、散布図を描くときは、どのような関係を検討したいかという目的を明確にし、その目的のために使うデータを工夫する必要があります。
うまく工夫すると、隠れていた関係が見えてくることがあります。

工夫することは大変です。でも、工夫するからこそ見えてくるものがあります!
散布図は、2つのデータの関係を検討したいときに役立つグラフですから、卒業論文や修士論文などを執筆するとき、積極的に活用することをお勧めします。
まとめ
散布図は、棒グラフや円グラフ、折れ線グラフよりも難しく感じるかもしれません。
でも、2つのデータ間の関係を検討したいときには、散布図を描いてみることをお勧めします。
ただし、散布図を描画するときは、まず、どのような関係を検討したいのかという目的を明確にしましょう。その目的のために、何と何の関係を描画するか工夫します。
うまく工夫できると、隠れていた関係が見えてくることがあります。

Excelを使うと、平均値の差の検定や相関係数の算出なども簡単にできます。ただし算出する際は「何を検討しようとしているのか」という目的を明確にすることが大切です!